Congruencia de triangulos

12. Congruencia de tr�angulos

12. Congruencia de tr�angulos

---

Corresponde a la sesi�n de GA 2.12. LOS GEMELOS

Al observar y comparar figuras geom�tricas, se advierte que, en algunos casos, dos de ellas tienen la misma forma pero no el mismo tama�o y, en otros, puede ser que sean de igual forma y tama�o. Al comparar dos figuras, si observamos que tienen la misma forma y la misma medida, decimos que las figuras son congruentes.

El s�mbolo que se emplea para denotar la congruencia es

Para comparar dos tri�ngulos y determinar si existe congruencia entre ellos, existen tres criterios, que se describen y ejemplifican a continuaci�n.

Primer criterio: lado, lado, lado (LLL)

Dos tri�ngulos son congruentes si los tres lados de uno de ellos son congruentes a los lados del otro tri�ngulo.

Segundo criterio: lado, �ngulo, lado (LAL)

Dos tri�ngulos son congruentes si, en el primer tri�ngulo, dos de sus lados y el �ngulo comprendido entre ellos del segundo tri�ngulo

Tercer criterio: �ngulo, lado, �ngulo (ALA)

Dos tri�ngulos son congruentes si dos �ngulos y el lado comprendido entre ellos, de uno de los tri�ngulos, son congruentes con dos de los �ngulos y el lado comprendido entre ellos del otro tri�ngulo.

Con la finalidad de ejemplificar los criterios de congruencia de los tri�ngulos, consid�rense los puntos que se dan a continuaci�n.

1. Los siguientes tri�ngulos son congruentes, lo cual puede comprobarse al medir los lados de cada tri�ngulo.

2. Los siguientes tri�ngulos no son congruentes, lo cual se comprueba al medir los lados de cada tri�ngulo.

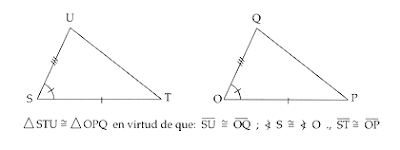
3. En los siguientes tri�ngulos, los segmentos y los �ngulos congruentes est�n marcados de la misma manera. En funci�n de tal circunstancia, es posible determinar en cu�l de los tres criterios de congruencia son LLL, LAL y ALA.

<

Como puede observarse, los tres lados del primer tri�ngulo son congruentes con los tres lados del segundo tri�ngulo; por lo tanto, estos tri�ngulos se identifican con el primer criterio de congruencia: lado, lado, lado (LLL).

Puede verse que estos tri�ngulos son congruentes debido a que presentan sus �ngulos y sus lados congruentes, respectivamente; por lo tanto, se identifican con el segundo criterio de congruencia: lado, �ngulo, lado (LAL).

Estos tri�ngulos tambi�n son congruentes, ya que dos �ngulos y el lado comprendido entre los �ngulos del primer tri�ngulo son congruentes con respecto al segundo tri�ngulo; por lo tanto, estos tri�ngulos se identifican con el tercer criterio de congruencia: �ngulo, lado, �ngulo (ALA).

Con base en el conocimiento de los criterios de congruencia se puede demostrar con facilidad cu�ndo dos tri�ngulos son congruentes.